 |
| AIOU |
Course: Analysis &
Design of Algorithms (3466) Semester: Autumn 2015
Level:
BS (CS) Total Marks: 100
Credit:
Half Credit Pass Marks: 50
ASSIGNMENT No. 1
Units: (1 – 4)
Note:
All
questions are compulsory. Each question carries equal marks.
Q. 1 a) Let c(n) and d(n) be
asymptotically positive functions. Prove or disprove each of the
following conjectures; (20)
-
c(n) = θ(c(n/2))
-
c(n) = O((c(n))2)
-
c(n) = O(d(n)) implies d(n) = Ω(c(n))
b) Prove that Pr{A | C} +
Pr{  | C} = 1.
| C} = 1.
Q.
2 a) Give examples of relations that are: (20)
-
Reflexive and Symmetric but not Transitive
-
Reflexive and Transitive but not Symmetric
-
Symmetric and Transitive but not Reflexive
-
Illustrate the operation of counting sort on the array A = [6, 0, 2, 0, 1, 3, 4, 6, 1, 3, 2].
Q.
3 a) Let A and B be finite sets, and f : A −> B be a function.
Show that: (20)
-
If f is injective, then |A| ≤ |B|
-
If f is surjective, then |A| ≥ |B|
b) Show that any connected,
undirected graph G = (V, E) satisfies |E| ≥ |V| - 1.
Q.
4 a) Illustrate
the operation of Heap sort on the array A = [5, 13, 2, 25, 7, 17, 20,
8, 4].
-
What is the running time of heap sort on an array A of length n that is already sorted in increasing order? What about decreasing order? (20)
Q.
5 Write notes on the following topics: (20)
ASSIGNMENT No. 2
Units:
(5 – 8)
Total
Marks: 100
Note:
All
questions are compulsory. Each question carries equal marks.
Q. 1 Give
and explain each step with graph example for the trace of following
graph traversal algorithms: (20)
Q. 3 a) Prove that thefractional knapsack problem has the greedy-choice property
b:What is an optimal Huffman code for the following set of frequencies, based on the first 8 Fibonacci numbers? (20)\
b:What is an optimal Huffman code for the following set of frequencies, based on the first 8 Fibonacci numbers? (20)\
Q. 4 Execute the following
algorithms for the given graph. Analyze the difference between the
order of nodes or edges visited for the two algorithms: (20)
a) Prim’s algorithm
b) Kruskal’s algorithm
Q. 5 Write notes on the
following topics: (20)
-
Hash Table and Functions
Analysis
and Design of Algorithm (3466/3503) Credit Hours: 3(3+0)
Recommended Book:
Introduction to Algorithms
by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
Course Outlines:
Unit No.1: Introduction
Introduction to Algorithm
Analysis and Design
Growth of Functions,
Summations Formulas and Properties
Unit No.2: Recurrences and
Sets
Substitution, Iteration and
Master Methods
Sets, Relations, Functions,
Graph and Trees, Counting and Probability
Unit No.3: Sorting
Algorithms
Heaps, Maintaining the Heap
Property, Heap Sort algorithm,
Quick Sort, Performance and
Analysis of Quick Sort
Unit No.4: Sorting in
Linear Time and Order Statistics
Lower bounds for sorting,
Counting sort, Radix and Bucket Sort, Medians and order Statistics
Unit No.5: Elementary Data
Structures
Analysis of Stack, Queues and
Linked List Algorithms, Hash Table and Functions, Binary Search Trees
Unit No.6: Dynamic
Programming
Matrix Chain Multiplication,
Longest Common Subsequence, Optimal Polygon Triangulation
Unit No.7: Greedy
Algorithms
An activity selection problem,
Huffman Codes, A Task Scheduling Problem, Amortized Analysis
Unit No.8: Graph Algorithms
Elementary Graph Algorithms,
Breadth first search, Depth first search, Minimum Spanning Trees
Unit No.9: Single Source
Shortest Paths
Shortest Paths and
Relaxation, Dijkstra’s Algorithm, The Bellman-Ford Algorithm,
Introduction to NP-Completeness
assginment No 1
assginment No 1











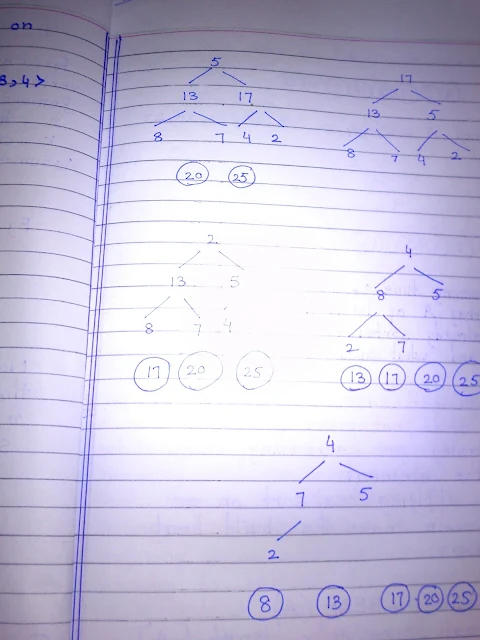

Although I know nothing about algorithms and codes and I don’t understand any of the math, but I do think the handwriting is pretty neat.
ReplyDelete